Implementing AES
11th April 2025
At last I’m ready to implement AES.
At its core the AES algorithm takes 128 bits of plain text and a secret key and encrypts the data into cipher text. This cipher text is an incomprehensible mess that is practically impossible to decipher unless you use the same secret key and the reverse AES algorithm to decrypt it.
AES uses various different methods to scramble the data. I'll explain each of these methods in turn but for now it's useful to know that these methods are used repeatedly in a loop and each time around that loop is called a round. I like to think of it like shuffling a deck of cards, you don't just shuffle once, you do it a number of times to make sure the deck is really messed up.
Another key property of AES is its heavy use of Galois Fields, especially GF(28). As a general rule, bytes are treated as vector arrays representing polynomials, and whenever addition or multiplication operations are performed, they are the operations from that field. This is why I spent so long learning about abstract algebra in preparation. I can’t overstate how much easier it is to understand AES if you have a good grasp of Galois Fields.
Enough preamble, let's get into the details.
S-boxes
One method AES uses to scramble data is a substitution box (s-box). This takes a number of input bits and replaces them with some number of output bits. This is typically implemented as a lookup table. AES uses an 8-bit to 8-bit s-box and can be implemented as a 256 element array, each element being an 8-bit value. Using the input as the index, the output is the element in the array at that index.
The creation of these s-boxes is tricky. It's important that no two input value maps to the same output. You don't want any value mapping to itself. Also it has to be nonlinear, which I translate to “unpredictable”, i.e. if you change one bit of the input you have no idea how many and which bits in the output will be affected.
Thankfully, we don't have to design the s-box, the authors of AES (Joan Daemen and Vincent Rijmen with some help from Kaisa Nyberg) already did that. And published it. We can just download the 256 values and paste them into our code, which would be perfectly acceptable and if that's what you want to do, go ahead. However they also published the process for generating the s-box and that seems like a lot more fun to me, so that's what I'm going to do.
The AES s-boxes use Galois Fields to do all the heavy lifting. The crux being the substitution value is the multiplicative inverse of the input value in GF(28) with the irreducible polynomial x8 + x4 + x3 + x + 1. As luck would have it, I already coded that in a previous post, here it is:
// Perform AES multiplication, i.e. polynomial multiplication in the field
// GF(256) with the irreducible polynomial x^8 + x^4 + x^3 + x + 1. Designed
// to work with 8 bit numbers despite the irreducible polynomial requiring 9
// bits.
static uint8_t aes_mul(uint8_t a, uint8_t b) {
uint8_t result = 0;
for (int i=0; i<8; i++) {
if (b & 0x01) {
result ^= a;
}
a = (a << 1) ^ (a & 0x80 ? 0x1b : 0);
b >>= 1;
}
return result;
}
// Perform polynomial division with 8 bit vectors.
static uint8_t poly_div(uint8_t a, uint8_t b, uint8_t* r) {
uint8_t mask = 0x80;
while (mask && !(mask & a) && !(mask & b)) {
mask >>= 1;
}
if (!(mask & a)) {
*r = a;
return 0;
}
uint8_t mag = 0;
while (mask && !(mask & b)) {
mask >>= 1;
mag++;
}
return (1 << mag) ^ poly_div(a ^ (b << mag), b, r);
}
// Perform polynomial division with the AES irreducible polynomial (which
// would normally require 9 bits) with an 8 bit vector.
static uint8_t aes_div(uint8_t b, uint8_t* r) {
uint8_t mask = 0x80;
uint8_t mag = 1;
while (mask && !(mask & b)) {
mask >>= 1;
mag++;
}
return (1 << mag) ^ poly_div(0x1b ^ (b << mag), b, r);
}
// Compute the AES multiplicative inverse using the Extended Euclidean Algorithm
static uint8_t aes_inverse(uint8_t r) {
uint8_t old_t = 0;
uint8_t t = 1;
uint8_t new_r;
uint8_t q = aes_div(r, &new_r);
while (new_r != 0) {
uint8_t new_t = old_t ^ aes_mul(q, t);
old_t = t;
t = new_t;
uint8_t old_r = r;
r = new_r;
q = poly_div(old_r, r, &new_r);
}
return t;
}To further thwart cryptanalysis the multiplicative inverse is then transformed using the following affine transformation where b is the multiplicative inverse as a vector and s is the s-box output.
This is matrix multiplication, I have the code for that too. Well almost, because the vector (of 8 bits) is actually stored as an integer, we need to do some bit manipulation to read and set individual bits. Also, because these bits represent coefficients in a polynomial, the calculations are performed in GF(2) so addition becomes an XOR and multiplication becomes an AND.
// read a bit
bool rbit(uint8_t value, unsigned int bit) {
return (value >> (bit)) & 1;
}
// set a bit
uint8_t sbit(uint8_t value, unsigned int bit, bool set) {
const uint8_t mask = 1 << (bit);
if (set) {
return value | mask;
} else {
return value & ~mask;
}
}
static uint8_t affine_matrix[8][8] = {
{1, 0, 0, 0, 1, 1, 1, 1},
{1, 1, 0, 0, 0, 1, 1, 1},
{1, 1, 1, 0, 0, 0, 1, 1},
{1, 1, 1, 1, 0, 0, 0, 1},
{1, 1, 1, 1, 1, 0, 0, 0},
{0, 1, 1, 1, 1, 1, 0, 0},
{0, 0, 1, 1, 1, 1, 1, 0},
{0, 0, 0, 1, 1, 1, 1, 1}
};
static uint8_t affine_transform(uint8_t vector) {
uint8_t result = 0;
for (size_t h=0; h<8; h++) {
uint8_t bit = 0;
for (size_t w=0; w<8; w++) {
bit ^= affine_matrix[h][w] & rbit(vector, w);
}
result = sbit(result, h, bit);
}
return result ^ 0x63;
}With that written we can now compute the s-box substitution for any particular byte.
static uint8_t sbox(uint8_t value) {
if (value==0) {
return 0x63;
}
return affine_transform(aes_inverse(value));
}Because zero has no multiplicative inverse, this is treated as a special case and given the value 99 (aka 63hex) which just so happens to be the only element not to appear anywhere else in the s-box.
But this is all terribly inefficient. The calculations involved, especially the division required for calculating the multiplicative inverse, are time consuming. It really would be better to use an array as a lookup table. So a compromise, I’ll compute the s-box values when the program first starts and store them in an array for later lookup. This way I'm not copying and pasting the table from Wikipedia, and I'm not needlessly computing the same expensive values over and over.
static uint8_t sbox[256] = {};
static void compute_sbox() {
sbox[0] = 0x63;
uint8_t value = 0;
do {
sbox[value] = affine_transform(aes_inverse(++value));
} while (value != 255);
}This also allows me to dump the s-box table to the console so I can double check I did everything correctly. I present those results here, so you can copy and paste them if you like :P
63 7c 77 7b f2 6b 6f c5 30 01 67 2b fe d7 ab 76 ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0 b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15 04 c7 23 c3 18 96 05 9a 07 12 80 e2 eb 27 b2 75 09 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84 53 d1 00 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf d0 ef aa fb 43 4d 33 85 45 f9 02 7f 50 3c 9f a8 51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2 cd 0c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73 60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e 0b db e0 32 3a 0a 49 06 24 5c c2 d3 ac 62 91 95 e4 79 e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 08 ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a 70 3e b5 66 48 03 f6 0e 61 35 57 b9 86 c1 1d 9e e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df 8c a1 89 0d bf e6 42 68 41 99 2d 0f b0 54 bb 16
While in software, like my web server, using a 256 byte array is the more efficient method, this is not always the case. In some implementations of AES there may not be 256 bytes of memory available to store the lookup. Examples include embedded systems or in hardware implementations. In these cases it may be preferable to compute the substitution on the fly as required.
Before moving on, the affine transformation can also be optimised, instead of performing a matrix multiplication you can use the sum of multiple circular shift operations of the input byte. Because the vector in this case is actually a byte, this is easier to code and quicker to execute.
uint8_t rotl(uint8_t value, unsigned int count) {
const unsigned int mask = CHAR_BIT * sizeof(value) - 1;
count &= mask;
return (value << count) | (value >> (-count & mask));
}
static void compute_sbox() {
sbox[0] = 0x63;
uint8_t value = 0;
do {
uint8_t inverse = aes_inverse(++value);
sbox[value] = inverse ^ rotl(inverse, 1) ^ rotl(inverse, 2) ^ rotl(inverse, 3) ^ rotl(inverse, 4) ^ 0x63;
} while (value != 255);
}I'm not 100% sure why the original matrix translates into those five rotations. My intuition says it's correct because the rows in the matrix consist of five 1s being circularly rotated, and while I tested it to make sure it generates the same results, I can't quite map it out in my head. No doubt this will bug me till I return to it and work out why, so maybe a future post on that.
Key expansion
AES supports three key sizes: 128, 192 or 256 bits. The key size dictates how many rounds the algorithm will perform, 10 for 128, 12 for 192 and 14 for 256. The add key operation is called once before the rounds start and once for each of the rounds. Each time the round key is 128 bits long, no matter the size of the initial key. With this information we can calculate how much key data we need. Also for reasons that will become clear in a minute, it's helpful to know this in multiples of 32-bit words instead of single bits.
| Initial key size (bits) |
Initial key size (32-bit words) |
Rounds | Round keys | Key data (bits) |
Key data (32-bit words) |
|---|---|---|---|---|---|
| 128 | 4 | 10 | 11 | 1408 | 44 |
| 192 | 6 | 12 | 13 | 1664 | 52 |
| 256 | 8 | 14 | 15 | 1920 | 60 |
AES uses a key schedule to expand the initial key into enough data for all the round keys. This algorithm is almost as involved as the rest of the AES algorithm, it's kind of like an algorithm nested inside an algorithm.
The key schedule is repetitive, repeating the same steps until the required amount of key data is produced. Each repetition is also called a round, but it's important to note these key schedule rounds are not related to the rounds in the main AES algorithm. For example, with a 192-bit key, each round in the key schedule generates 192 bits of data. This requires a total of 8 rounds to generate all required data. However the main AES rounds consume the key data at 128 bits of data per round, requiring a total of 12 rounds after the extra initial key add.
The algorithm is similar for all three key lengths, but for ease of explanation I shall start with the 128-bit key. The key schedule operates on 32-bit words, so for the 128-bit key there will initially be four 32-bit words and we need a total of 44 words. Each round of the key schedule generates four words, so a total of 11 rounds are needed.
The first round is simple, the first four words (w0 to w3) are a copy of the four words from the initial key. The subsequent rounds generate the next four words by adding the previous word (wi-1) to the word from the previous round (wi-4). This addition is performed in GF(232) so the addition translates into a bitwise XOR.
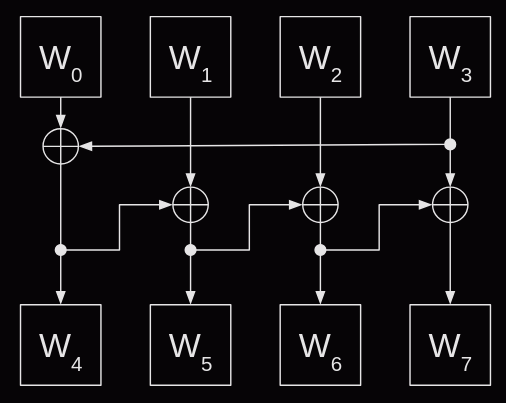
Except it's not quite that easy. The first word in each round actually goes through some extra transformations.
- Take the previous word (wi-1).
- Rotate the bytes in that word one to the left.
- Apply the s-box substitution to each byte in that word.
- Add a round constant to the high order byte. (More on this in a moment).
- Add to the word from the previous round (wi-4).
The corrected diagram:
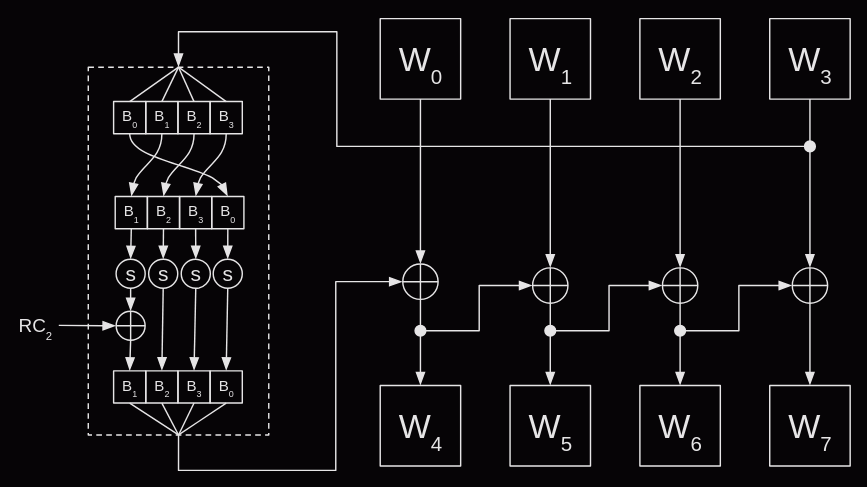
The round constant is a member of GF(23). It starts with the value 1 for the second round (it's not required for the first round which is a straight copy of the initial key). For each subsequent round it is multiplied by x. By round nine the round constant will be x7. For round ten, the multication by x will wrap around to x4 + x3 + x + 1. For reference this table gives the hex values for the round constant in each round.
| Round: | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Round Constant (hex): | 01 | 02 | 04 | 08 | 10 | 20 | 40 | 80 | 1b | 36 |
Expressed as code, key expansion looks like this:
// Key expansion
static void copy_word(uint8_t dest[4], uint8_t src[4]) {
for (size_t i=0; i<4; i++) {
dest[i] = src[i];
}
}
static void add_word(uint8_t dest[4], uint8_t word[4]) {
for (size_t i=0; i<4; i++) {
dest[i] ^= word[i];
}
}
static void rotate_word(uint8_t word[4]) {
uint8_t temp = word[0];
for (size_t i=0; i<3; i++) {
word[i] = word[i+1];
}
word[3] = temp;
}
static void sub_word(uint8_t word[4]) {
for (size_t i=0; i<4; i++) {
word[i] = sbox[word[i]];
}
}
static uint8_t* expand_key(uint8_t* key, uint8_t* initial_key) {
// initial key
for (size_t i=0; i<4; i++) {
copy_word(key + (i*4), initial_key + (i*4));
}
// expand
uint8_t rc = 0x01;
for (size_t i=4; i<44; i++) {
uint8_t* current_word = key + (i*4);
uint8_t* prev_word = key + ((i-1)*4);
uint8_t* prev_round = key + ((i-4)*4);
copy_word(current_word, prev_word);
if (i%4 == 0) {
rotate_word(current_word);
sub_word(current_word);
current_word[0] ^= rc;
rc = aes_mul(rc, 0x02);
}
add_word(current_word, prev_round);
}
return key;
}The code is not quite as clean as I would like, this is mainly because some of the operations work on 32-bit words and some on 8-bit bytes. Storing the key as an array of 8-bit numbers as I’ve done above means some extra loops and some pointer arithmetic to convert from a word index to a byte index. Alternatively, storing the keys as an array of 32-bit numbers presents complications when wanting to manipulate a specific 8-bit byte for the s-box and round constant steps. In the end I went with the 8-bit route because the rest of the AES algorithm uses 8-bit bytes.
For a key length of 192, the algorithm is very similar. The initial key is six words long and we need a total of 52. This time, each round will generate six words. In general the round length will match the length of the initial key. As before the first round is a straight copy of the initial key. The first word in the subsequent rounds performs the more complex rotate-sub-add operations and the other five the simpler add operation.
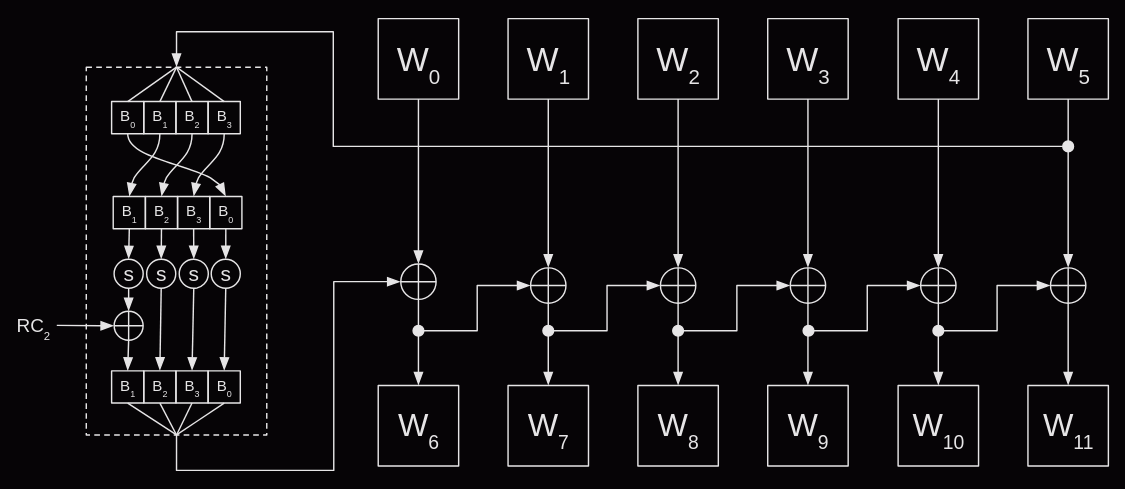
The original code can be modified to work with both key sizes by replacing the hard coding with parameters defining the initial key length and total number of words required.
static uint8_t* expand_key(uint8_t* key, uint8_t* initial_key, size_t starting_words, size_t total_words) { // initial key for (size_t i=0; i<starting_words; i++) { copy_word(key + (i*4), initial_key + (i*4)); } // expand uint8_t rc = 0x01; for (size_t i=starting_words; i<total_words; i++) { uint8_t* current_word = key + (i*4); uint8_t* prev_word = key + ((i-1)*4); uint8_t* prev_round = key + ((i-starting_words)*4); copy_word(current_word, prev_word); if (i%starting_words== 0) { rotate_word(current_word); sub_word(current_word); current_word[0] ^= rc; rc = aes_mul(rc, 0x02); } add_word(current_word, prev_round); } return key; }
The algorithm for 256-bit keys is almost the same, the predictable difference being the algorithm now generates eight words per round. There is however an extra twist, the fifth word in each round is not a simple addition any more, instead the bytes of wi-1 are first substituted using the s-box.
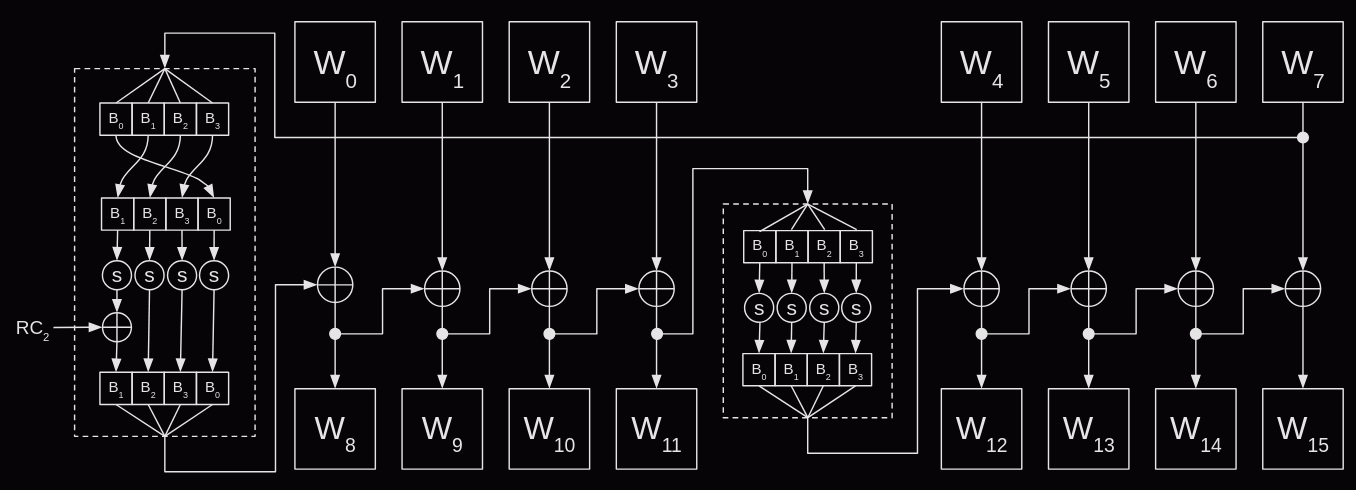
This requires a minor update to the code, an extra branch to check for this condition and perform the extra substitutions.
static uint8_t* expand_key(uint8_t* key, uint8_t* initial_key, size_t starting_words, size_t total_words) { // initial key for (size_t i=0; i<starting_words; i++) { copy_word(key + (i*4), initial_key + (i*4)); } // expand uint8_t rc = 0x01; for (size_t i=starting_words; i<total_words; i++) { uint8_t* current_word = key + (i*4); uint8_t* prev_word = key + ((i-1)*4); uint8_t* prev_round = key + ((i-starting_words)*4); copy_word(current_word, prev_word); if (i%starting_words == 0) { rotate_word(current_word); sub_word(current_word); current_word[0] ^= rc; rc = aes_mul(rc, 0x02);} else if (starting_words == 8 && i%4 == 0) { sub_word(current_word); }add_word(current_word, prev_round); } return key; }
Encryption
With the s-box built and the key expanded, we are ready to start encrypting data.
Conceptually the data is divided into 16 (8-bit) bytes, and the 16 bytes are arranged in a four by four grid as shown below.
| B0 | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 | B13 | B14 | B15 |
↓
| B0 | B4 | B8 | B12 |
| B1 | B5 | B9 | B13 |
| B2 | B6 | B10 | B14 |
| B3 | B7 | B11 | B15 |
The algorithm starts by adding the first 128-bits from the key schedule to the data. It then performs its main loop scrambling the data for a number of rounds depending on the key length. All the rounds are the same except the last one which skips a step for some reason. Here is the breakdown of all the steps performed:
Which translates quite nicely to code.
static void encrypt(uint8_t block[16], size_t rounds, uint8_t* key) {
add_key(block, key);
for (size_t round=1; round<=rounds; round++) {
sub_bytes(block);
shift_rows(block);
if (round<rounds) {
mix_columns(block);
}
add_key(block, key+(round*16));
}
}We now just need to write the individual steps.
Add round key
All the hard work for this step is already done. The key expansion has generated the round keys and the high level encryption function has selected the correct round key. All that is left to do is take the round key and add (XOR) it with the data.
static void add_key(uint8_t block[16], uint8_t key[16]) {
for (size_t i=0; i<16; i++) {
block[i] ^= key[i];
}
}Sub bytes
The hard work for this step is also done. This simply becomes a loop substituting each byte using the s-box lookup table.
static void sub_bytes(uint8_t block[16]) {
for (size_t i=0; i<16; i++) {
block[i] = sbox[block[i]];
}
}Shift rows
Remember that the data in AES is conceptually arranged in a four by four grid of bytes. This step moves the bytes in each row about, technically it rotates them.
| B0 | B4 | B8 | B12 |
| B1 | B5 | B9 | B13 |
| B2 | B6 | B10 | B14 |
| B3 | B7 | B11 | B15 |
| No change |
| Rotate 1 to the left |
| Rotate 2 to the left |
| Rotate 3 to the left |
| B0 | B4 | B8 | B12 |
| B5 | B9 | B13 | B1 |
| B10 | B14 | B2 | B6 |
| B15 | B3 | B7 | B11 |
My instinct here was to use some kind of bit shifting to achieve this, but because the bytes in each row are spread out over the actual array of data (for example the second row consists of bytes 1, 5, 9 and 13) this would not work. I couldn't think of anything smarter than to just hard code the shift for each row.
static void shift_rows(uint8_t block[16]) {
// row 2
uint8_t temp = block[1];
block[1] = block[5];
block[5] = block[9];
block[9] = block[13];
block[13] = temp;
// row 3
temp = block[2];
block[2] = block[10];
block[10] = temp;
temp = block[6];
block[6] = block[14];
block[14] = temp;
// row 4
temp = block[15];
block[15] = block[11];
block[11] = block[7];
block[7] = block[3];
block[3] = temp;
}Mix columns
This step performs matrix multiplication against each column, treating the column as a 4 element vector.
The code for this uses a variation of the matrix multiplication from the last post, the modification being the normal arithmetic is replaced with operations for GF(23). Additionally once the new vector (column) is computed it is written back over the original vector.
static uint8_t columns_matrix[4][4] = {
{2, 3, 1, 1},
{1, 2, 3, 1},
{1, 1, 2, 3},
{3, 1, 1, 2}
};
static void mix_column(uint8_t block[4]) {
uint8_t result[4];
for (size_t h=0; h<4; h++) {
result[h] = 0;
for (size_t w=0; w<4; w++) {
result[h] ^= aes_mul(columns_matrix[h][w], block[w]);
}
}
for (size_t i=0; i<4; i++) {
block[i] = result[i];
}
}
static void mix_columns(uint8_t block[16]) {
for (size_t i=0; i<4; i++) {
mix_column(block + (i*4));
}
}Victory?
That's it, we are done, we can now encrypt data using AES.
Except we are not really done. For a start, we can only encrypt exactly 16 bytes (128 bits) of data. Conveniently my test string was 16 characters long, but what if we want to encrypt more? Or less? And how do we go about decrypting it?
Decryption
Let's start with decryption, that should be easy really, just do everything I've described so far backwards.
Well not quite everything is backwards. The key expansion is performed exactly the same as before, but the round keys are used in reverse order.
Sub bytes is reversed. To compute the reverse substitution we need to first perform the reverse affine transformation (the matrix multiplication below), then find the multiplicative inverse.
We need to take care with 63hex which after the reverse affine transformation will be zero which has no multiplicative inverse. Instead 63hex is substituted with 00hex. This should be no surprise as the forward s-box maps 00hex to 63hex.
There is however a cheat, we don’t need to compute the inverse s-box this way. When computing the normal forward s-box array, we can also populate the inverse s-box array by swapping the index and values.
// AES S-box values static uint8_t forward_sbox[256] = {};static uint8_t inverse_sbox[256] = {};static void compute_sbox() { forward_sbox[0] = 0x63;inverse_sbox[0x63] = 0;uint8_t value = 0; do { uint8_t inverse = aes_inverse(++value); forward_sbox[value] = inverse ^ rotl(inverse, 1) ^ rotl(inverse, 2) ^ rotl(inverse, 3) ^ rotl(inverse, 4) ^ 0x63;inverse_sbox[forward_sbox[value]] = value;} while (value != 255); }
Shift rows is also reversed, where before we rotated left, now we rotate right.
static void inverse_shift_rows(uint8_t block[16]) {
// row 1
uint8_t temp = block[13];
block[13] = block[9];
block[9] = block[5];
block[5] = block[1];
block[1] = temp;
// row 2
temp = block[2];
block[2] = block[10];
block[10] = temp;
temp = block[6];
block[6] = block[14];
block[14] = temp;
// row 3
temp = block[3];
block[3] = block[7];
block[7] = block[11];
block[11] = block[15];
block[15] = temp;
}The code for the reversed mix columns is basically the same. Each column is multiplied by a matrix. The only difference is the matrix being used, we now need to use the following inverse matrix.
Finally the algorithm as a whole performs the rounds and steps in the reverse order.
static void decrypt(uint8_t block[16], size_t rounds, uint8_t* key) {
for (size_t round=rounds; round>=1; round--) {
add_key(block, key+(round*16));
if (round<rounds) {
mix_columns(block, inverse_columns_matrix);
}
inverse_shift_rows(block);
sub_bytes(block, inverse_sbox);
}
add_key(block, key);
}Modes of operation
Modes of operation are algorithms that wrap around AES to expand its use beyond the basic blocks of 128 bits. There are several modes of operation but for now I'm going to focus on two, ECB and CBC.
ECB or Electronic Code Book simply breaks the input data into 128-bit blocks and encodes each one in turn using AES. It's the obvious naive solution. It has problems cryptographically because the same message with the same key will produce the same cipher text. A duplicated 128-bit block in the message will also generate identical 128-bit cipher text. This opens this algorithm up to cryptanalysis.
ECB is also vulnerable to manipulation. While attackers may not be able to decipher blocks they could replace individual blocks undetected. If for example a bad actor works out that the second block of a message between banks describing a money transfer contains the destination account number, they could replace that block to redirect the transfer.
Granted, this analysis and manipulation requires a considerable effort and a little luck, but it's possible and can be avoided with a different mode of operation. The objective here is to first prevent two identical messages being encrypted into the same cipher text and thus prevent observers from spotting patterns and performing analysis. Second, prevent manipulation by allowing bad actors to replace blocks undetected.
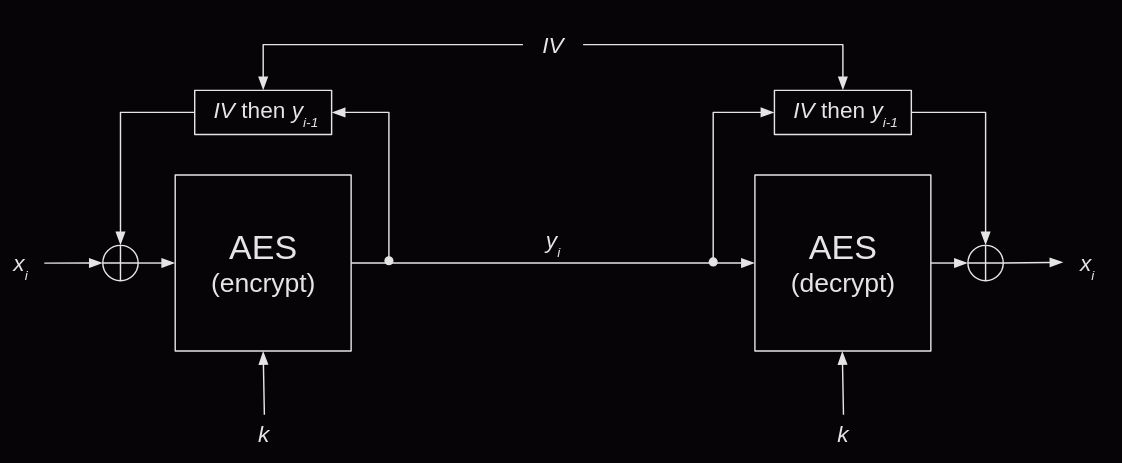
CBC or Cipher Block Chaining still breaks the input into 128-bit blocks but before encrypting each block the plain text is XORed with another block. For most of this algorithm the other block is the cipher text from the previous block, hence the Cipher Block Chaining name as each block is linked to the previous block. For the first block a random initial value is required, this is called the Initialisation Vector or IV. It is important that this IV is never used for more than one message. The random IV means duplicate messages will result in different cipher texts. The chaining means blocks cannot be replaced without corrupting the message.
When decrypting the message, the blocks need to be XORed after deciphering with the AES algorithm. The same IV needs to be used for the first block, and the cipher text of the previous block for all the others. Unlike the key, the IV does not need to be kept secret and can be transmitted in the clear.
static void cbc_encrypt(size_t rounds, uint8_t* key, uint8_t iv[16], FILE *input_file, FILE *output_file) {
uint8_t block[16];
uint8_t cb[16];
size_t read;
memcpy(cb, iv, 16);
do {
read = fread(block, 1, 16, input_file);
add_blocks(block, cb);
encrypt(block, rounds, key);
memcpy(cb, block, 16);
fwrite(block, 1, 16, output_file);
} while (read==16);
}
static void cbc_decrypt(size_t rounds, uint8_t* key, uint8_t iv[16], FILE *input_file, FILE *output_file) {
uint8_t block[16];
uint8_t cb[16];
uint8_t next_cb[16];
size_t read;
memcpy(next_cb, iv, 16);
while ((read = fread(block, 1, 16, input_file)) == 16) {
memcpy(cb, next_cb, 16);
memcpy(next_cb, block, 16);
decrypt(block, rounds, key);
add_blocks(block, cb);
fwrite(block, 1, 16, output_file);
}
}Padding
Both these modes of operations rely on the data being an exact multiple of 16 bytes (aka 128 bits). This is obviously not the case most times. Everything being equal, 15 out of 16 times, the last block is going to be less than 16 bytes. This is where padding is required to fill out the last block.
There are multiple ways of doing this. The naive solution is to set the remaining bytes to 0 or a null byte. This encrypts fine but is difficult to decrypt as you can't be sure if the trailing byte is padding or a genuine null byte from the original plain text.
Another solution is to set the first padding byte to 80hex (10000000bin), and the remaining bytes to 0. This value, 80hex, is defined as the padding character in unicode. It is therefore easy to detect when decrypting if the source message was unicode encoded text. If it's ASCII it might work, if it's binary data we can't always be sure if it's a valid byte or padding.
Yet another solution is to pad to the remaining bytes with the number of padded bytes. For example if the last block has 11 bytes of data, the last 5 bytes are set to the value 5. When decrypting the last block, the last byte will be the number of bytes that can be removed as padding. If the message is an exact multiple of 16 bytes, there should be 0 padding but equally no where to store that value. In these circumstances, the message is instead padded with an extra block with all bytes being set to 16.
This method is called PKCS7 and seems to be the method most often used with ECB and CBC so is the method I've coded.
static void pkcs_pad(uint8_t block[16], size_t len) { uint8_t pad = 16 - len; for (size_t i=len; i<16; i++) { block[i] = pad; } }static void cbc_encrypt(size_t rounds, uint8_t* key, uint8_t iv[16], FILE *input_file, FILE *output_file) { uint8_t block[16]; uint8_t cb[16]; size_t read; memcpy(cb, iv, 16); do { read = fread(block, 1, 16, input_file);if (read<16) { pkcs_pad(block, read); }add_blocks(block, cb); encrypt(block, rounds, key); memcpy(cb, block, 16); fwrite(block, 1, 16, output_file); } while (read==16); } static void cbc_decrypt(size_t rounds, uint8_t* key, uint8_t iv[16], FILE *input_file, FILE *output_file) { uint8_t block[16];uint8_t next_block[16];uint8_t cb[16]; uint8_t next_cb[16]; size_t read; memcpy(next_cb, iv, 16);read = fread(block, 1, 16, input_file); while (read == 16) {memcpy(cb, next_cb, 16); memcpy(next_cb, block, 16); decrypt(block, rounds, key); add_blocks(block, cb);read = fread(next_block, 1, 16, input_file); if (read == 16) { fwrite(block, 1, 16, output_file); } else { fwrite(block, 1, 16-block[15], output_file); } memcpy(block, next_block, 16);} }
Crypto
For testing I've wrapped all this code into a new executable called “crypto”. This is a basic command line tool that performs encryption and decryption using AES. The code beyond what has already been described above wrangles the command line parameters, handles IO and calls the appropriate AES encrypt or decrypt function.
I did this instead of trying to integrate it into Tinn because this is just a small part of TLS/HTTPS and trying to test this in isolation on a web server didn't make sense.
You can find a complete listing of crypto on github. If you decide to clone and build it for yourself, please don't trust it for anything real. While I'm confident it works, it has had no kind of actual review, it may well be leaking data all over the place.
Next
There are a bunch of optimisations I could make to this code. Chiefly I can combine a lot of the steps in each round into fewer operations. For example I could combine the sub bytes and shift rows steps into one and half the number of loops I need. Beyond this there are optimisations that can be made by processing each block as 4 32-bit words instead of 16 8-bit bytes. These changes make the code harder to follow, which is why I've not done it. It would make it faster and more efficient, but if that was my concern I should use a pre-existing library that has been optimised and tested by the wider community. I might visit these topics later, but for now I'm moving on.
AES is known as a symmetric encryption algorithm because it uses the same key for encryption and decryption. The big problem with AES and all symmetric encryption algorithms is key distribution. How do you get the secret key to the intended recipient without bad actors intercepting it and then having the ability to decipher all your secret messages? Well that's where asymmetric encryption algorithms come to the rescue and where I must journey next.
TC